ビンゴバルーン最適解を計算

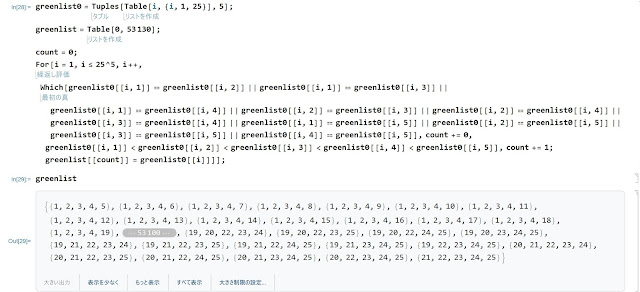
 だいぶん昔にやったので、{1,2,3,4,5}⇔1,{21,22,23,24,25}⇔53130などの対応をする関数を以前作ったのだが←方向の変換が消えていたので別プログラムで急遽作った。

ビンゴファームを作った時の流用なので緑カードという意味のgreenlistとなっているが気にしない。これはとりあえず1~25を重複アリでもよいのでこの中からとってきた要素を5つ持つ集合のリストを生成。これは25^5個の集合である。なおこれはおよそ1000万個の集合である。

ここから、各要素が等しい場合を除き(例えば{1,2,3,3,4}は３番目と４番目が等しいので除去、{1,2,3,3,3}は3,4,5番目が等しいが、||は「または」を意味するので３番目と４番目が等しいという条件にすでにひっかかり除去。)加えて昇順である条件を付けると、簡単に{1,2,3,4,5}をはじめとして{21,22,23,24,25}を最後とする25C5=53130通りのデータが出来上がる。

これをシンキングタイムにまでに入ったマスの位置とする。

スマホアプリにおいては外部からの画像判定を使う予定である。

できるかわからんが…。

そしてすでに手元にある、CPUをフルで稼働させて１か月くらいかかった超貴重なデータをmathematicaに入力し、残り３球の1140通りに対し厳密な確率を計算する。

おそらく有用なデータとしては、配当獲得率、等倍以上、３倍以上、５倍以上、１０倍以上、３０倍以上、５０倍以上、７個ライン成立率、☆獲得効率、平均ＰＯ率(各ＦＲＥＥ配置可能個数別)と、配置すべきバルーンの位置を示した直感的な画像だろう。

アプリで逐一これを計算させると時間がかかってシンキング中に答えを出せないようではごみアプリなのでここはあらかじめ計算させたデータで一瞬で表示できるようにしたい。

次の記事では実際に上記事項をプログラミングし、それらがデータとして得られることを示す。