ものすごく久しぶりになったが、最近の様子を報告すると…。
当時持っていた不安が全然なく、底なしの元気かと言われていた時代はとっくに終わりをつげ、最近はあまり調子は悪くもなく、良くもなくといった感じである。
なおこのブログは自分の歴史を振り返るときに、大いに参考にさせたいただいた。
最近やるべきことはそこまで去年などの入試時代と違い多くないので、楽ではあるが…。
レゴを作成したり、プログラミングで遊んだりしている。
例えばアニマロッタのチェーンボンバーの払い戻し率を計算できるプログラムを作ったりした。
dataset = 1; oddslist = Table[Table[0, 10000], dataset]; counter =
Table[Table[0, 1001], dataset]; For[game = 1, game <= dataset, game++,
totalodds = 0; maxodds = 0;
For[times = 1, times <= 100000, times++, oddsupinitial = 0;
rowodds = {1.5, 0.6, 0.5, 0.5, 0.6, 1.5};
basicrowodds = {1.5, 0.6, 0.5, 0.5, 0.6, 1.5}; maxchain = 1;
chain = 1; oddsup1 = RandomInteger[{2, 5}];
oddsup2 = RandomInteger[{1, 2}];
Which[oddsup2 == 1, oddsup2 = 1, oddsup2 == 2, oddsup2 = 6];
pattern = allpattern[[game]];
in = {1, 2, 3, 4, 5, 6, 7, 8};
pattern[[RandomInteger[{31, 54}]]] = 6;
random = RandomInteger[{1, 10}];
If[random == 1, pattern[[RandomInteger[{31, 54}]]] = 6];
syokipattern = pattern;
numlist = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
For[i = 1, i <= 100, i++, randomA = RandomInteger[{1, 54}];
randomB = RandomInteger[{1, 54}];
taihi = numlist[[randomA]];
numlist[[randomA]] = numlist[[randomB]];
numlist[[randomB]] = taihi];
syokinumlist = numlist;
For[a = 1, a <= 5, a++, chain = 1; bomblist = Table[0, 54];
erase = Table[0, 54]; k1 = k2 = k3 = k4 = k5 = k6 = 0;
bombwait1 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
bombwait2 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
bombwait3 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
bombwait4 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
bombwait5 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
bombwait6 = {0, 0, 0, 0, 0, 0, 0, 0, 0};
precount = 0; postcount = 1; bombflag = 0;
Which[a == 1,
For[b = 1, b <= 54, b++,
If[numlist[[b]] == in[[1]] || numlist[[b]] == in[[2]] ||
numlist[[b]] == in[[3]],
Which[pattern[[b]] == 6, bombflag = 1; mass = b,
pattern[[b]] < 6, numlist[[b]] = 0; pattern[[b]] = 0]]],
a == 2, For[b = 1, b <= 54, b++,
If[numlist[[b]] == in[[4]] || numlist[[b]] == in[[5]],
Which[pattern[[b]] == 6, bombflag = 1; mass = b,
pattern[[b]] < 6, numlist[[b]] = 0; pattern[[b]] = 0]]],
a == 3, For[b = 1, b <= 54, b++,
If[numlist[[b]] == in[[6]],
Which[pattern[[b]] == 6, bombflag = 1; mass = b,
pattern[[b]] < 6, numlist[[b]] = 0; pattern[[b]] = 0]]],
a == 4, For[b = 1, b <= 54, b++,
If[numlist[[b]] == in[[7]],
Which[pattern[[b]] == 6, bombflag = 1; mass = b,
pattern[[b]] < 6, numlist[[b]] = 0; pattern[[b]] = 0]]],
a == 5, For[b = 1, b <= 54, b++,
If[numlist[[b]] == in[[8]],
Which[pattern[[b]] == 6, bombflag = 1; mass = b,
pattern[[b]] < 6, numlist[[b]] = 0; pattern[[b]] = 0]]]];
If[bombflag == 1, b = mass;
For[e = 1, e <= 1, e++, bomblist[[b]] = 1;
While[precount < postcount,
For[c = 1, c <= 54, c++, precount = postcount;
For[d = 1, d <= Length[nextlist[b]], d++,
If[pattern[[nextlist[b][[d]]]] == 6,
bomblist[[nextlist[b][[d]]]] = 1]];
If[bomblist[[c]] == 1,
For[d = 1, d <= Length[nextlist[c]], d++,
If[pattern[[nextlist[c][[d]]]] == 6,
bomblist[[nextlist[c][[d]]]] = 1]];]];
postcount = Count[bomblist, 1]]; kibaku = Table[0, 54];
For[f = 1, f <= 54, f++,
If[bomblist[[f]] == 1, kibaku[[f]] = 1; pattern[[f]] = 0;
numlist[[f]] = 0;
For[g = 1, g <= Length[nextlist[f]], g++,
tonari = nextlist[f][[g]]; pattern[[tonari]] = 0;
kibaku[[tonari]] = 1]]];
For[f = 1, f <= 54, f++,
If[kibaku[[f]] == 1 && bomblist[[f]] != 1 && numlist[[f]] > 0,
retu = QuotientRemainder[f, 6][[2]]; If[retu == 0, retu = 6];
Which[retu == 1, k1 += 1; bombwait1[[k1]] = numlist[[f]],
retu == 2, k2 += 1; bombwait2[[k2]] = numlist[[f]], retu == 3,
k3 += 1; bombwait3[[k3]] = numlist[[f]], retu == 4, k4 += 1;
bombwait4[[k4]] = numlist[[f]], retu == 5, k5 += 1;
bombwait5[[k5]] = numlist[[f]], retu == 6, k6 += 1;
bombwait6[[k6]] = numlist[[f]]];]];
For[h = 1, h <= 54, h++,
If[kibaku[[h]] == 1 || bomblist[[h]] == 1, pattern[[h]] = 0;
numlist[[h]] = 0]]];];
chainflag = 0; While[chainflag == 0, chainflag = 1;
For[i = 48, i >= 1, i--, nullcount = 0;
If[pattern[[i]] != 0 ,
For[j = i + 6, j <= 54, j = j + 6,
If[pattern[[j]] == 0, nullcount += 1]]];
If[nullcount > 0, pattern[[i + 6*nullcount]] = pattern[[i]];
numlist[[i + 6*nullcount]] = numlist[[i]]; pattern[[i]] = 0;
numlist[[i]] = 0]]; erase = Table[0, 54]; chaincount = 0;
For[i = 1, i <= 54, i++,
If[pattern[[i]] != 0 && pattern[[i]] < 6,
For[j = 1, j <= Length[nextlist[i]], j++,
If[pattern[[nextlist[i][[j]]]] == pattern[[i]],
erase[[nextlist[i][[j]]]] = 1; chainflag = 0;
If[chaincount == 0, chain += 1; chaincount = 1];
If[numlist[[nextlist[i][[j]]]] != 0 &&
bombcheck[[nextlist[i][[j]]]] == 0,
Which[QuotientRemainder[nextlist[i][[j]], 6][[2]] == 1,
k1 += 1; bombwait1[[k1]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1,
QuotientRemainder[nextlist[i][[j]], 6][[2]] == 2, k2 += 1;
bombwait2[[k2]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1,
QuotientRemainder[nextlist[i][[j]], 6][[2]] == 3, k3 += 1;
bombwait3[[k3]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1,
QuotientRemainder[nextlist[i][[j]], 6][[2]] == 4, k4 += 1;
bombwait4[[k4]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1,
QuotientRemainder[nextlist[i][[j]], 6][[2]] == 5, k5 += 1;
bombwait5[[k5]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1,
QuotientRemainder[nextlist[i][[j]], 6][[2]] == 0, k6 += 1;
bombwait6[[k6]] = numlist[[nextlist[i][[j]]]];
bombcheck[[nextlist[i][[j]]]] = 1]]]]]];
bombcheck = Table[0, 54];
For[i = 1, i <= 54, i++,
If[erase[[i]] == 1, pattern[[i]] = 0; numlist[[i]] = 0]]];
If[chain > maxchain, maxchain = chain];
doubletimes = 0;
If[chain >= 5, doubletimes = chain - 4];
For[n = 1, n <= doubletimes, n++,
Which[oddsupinitial == 0,
rowodds[[oddsup1]] += basicrowodds[[oddsup1]]; oddsupinitial = 1,
oddsupinitial == 1,
rowodds[[oddsup2]] += basicrowodds[[oddsup2]]]];
bottom = {0, 0, 0, 0, 0, 0};
k = {k1, k2, k3, k4, k5, k6};
l = {0, 0, 0, 0, 0, 0};
bombwait = {bombwait1, bombwait2, bombwait3, bombwait4, bombwait5,
bombwait6};
For[i = 1, i <= 6, i++, l[[i]] = 9;
For[j = 48 + i, j >= 1, j = j - 6,
Which[pattern[[j]] == 0, bottom[[i]] = l[[i]], pattern[[j]] != 0,
l[[i]] = l[[i]] - 1]]];
For[i = 1, i <= 6, i++, m = 0;
For[j = l[[i]] - k[[i]] + 1, j <= l[[i]], j++, m += 1;
pattern[[6*j + i - 6]] = 6;
numlist[[6*j + i - 6]] = bombwait[[i, m]]]]];
eraseline = {0, 0, 0, 0, 0, 0};
For[a = 1, a <= 6, a++,
Which[pattern[[48 + a]] == 0, eraseline[[a]] = 1,
pattern[[48 + a]] != 0, eraseline[[a]] = 0]];
odds = eraseline[[1]]*rowodds[[1]] + eraseline[[2]]*rowodds[[2]] +
eraseline[[3]]*rowodds[[3]] + eraseline[[4]]*rowodds[[4]] +
eraseline[[5]]*rowodds[[5]] + eraseline[[6]]*rowodds[[6]];
If[eraseline == {1, 1, 1, 1, 1, 1}, odds += 50]; totalodds += odds;
odds10 = odds*10; counter[[game, 1 + odds10]] += 1
; PO = totalodds/times; oddslist[[game, times]] = odds;
If[odds > maxodds, maxodds = odds];
If[QuotientRemainder[times, 1000][[2]] == 0,
Print[{game, times, maxchain, odds, PO, maxodds}]]
;]; counter[[game, 1001]] = PO]; export =
Table[Table[0, 1065], dataset]; For[i = 1, i <= dataset, i++,
export[[i, 1]] = i;
export[[i, 2]] = data[[1, i + 2, 5]]/10;
export[[i, 3]] = counter[[i, 1001]];
For[j = 4, j <= 57, j++, export[[i, j]] = allpattern[[i, j - 3]]];
over0 = over1 = over3 = over5 = over10 = over30 = over50 = 0;
For[k = 1, k <= 10000, k++, hantei = oddslist[[i, k]];
If[hantei > 0, over0 += 1]; If[hantei >= 1, over1 += 1];
If[hantei >= 3, over3 += 1];
If[hantei >= 5, over5 += 1];
If[hantei >= 10, over10 += 1];
If[hantei >= 30, over30 += 1];
If[hantei >= 50, over50 += 1];];
export[[i, 58]] = over50;
export[[i, 59]] = over30;
export[[i, 60]] = over10;
export[[i, 61]] = over5;
export[[i, 62]] = over3;
export[[i, 63]] = over1;
export[[i, 64]] = over0;
For[j = 1, j <= 1000, j++, export[[i, j + 64]] = counter[[i, j]]];
export[[i, 1065]] =
data[[1, i, 5]]]; Export["data.csv", export]; SystemOpen["data.csv"]
だいたい自身のやりたいアニマロッタ5の再現は以前の記事で紹介したので、
今度は数値的な解析などをして遊んでいる。
ちなみにチェーンボンバーは払い戻しが平均70%程度で、話にならない。
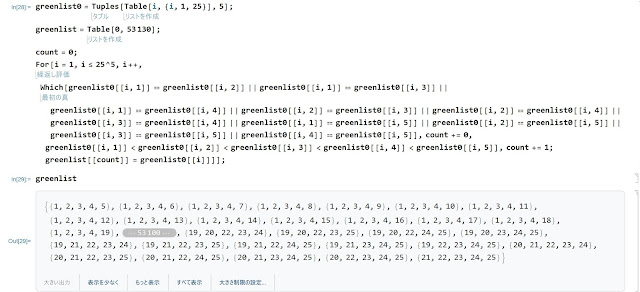
ビンゴファームも解析中で各パターン100000回検証をしているが、ペイアウト率は55%程度以上は確保されているが80%以上の組み合わせがなかなかない模様。
なにしろ緑カードパターンは17種類なので、組み合わせは17*16*15*14通りもあるので調べ上げるのに数十日レベルでかかるとみられている。
(カード配置パターンはその位置によって変わるので、17C4でもないし、重複はないので17^4でもない)
このあたりの話も話すとあまりに長くなるのでいずれ述べる…かもしれない
また、試験的に広告を貼るとかいう行為をやりだすことに。
ただ今度は、以前のように何度も日記のようなことを書くわけではない。
気が向いたときに面白そうなことを書くだけであろういんぷ
ちなみにプログラミングでいろいろ遊ぶのが大好きではあるが、工学系の学部にいるわけではない。わかる人にはわかると思うが、6年制の大学であり、試験や覚えることが山ほどあり、国家試験すら必要な学科である。
我はここでこういった理学系の知識を活かしつつ、社会と研究の橋渡しをいずれはしたいと考えている。入試の面接でもそう言ってきた。
また最近の動向もおいおい伝えていくが、例にもれず突然の失踪もありうるので注意。
一応このブログと広告がどんな感じにリンクして、どういう感じの統計になるかも見てみようと思っている。